The NTP Era and Era Numbering
Last update: June 24, 2022 20:19 UTC (fc65ae47b)

from The Wizard of Oz, L. Frank Baum
Era dynamically aloft
Table of Contents
Abstract
The Network Time Protocol (NTP) specification defines the timescale in terms of timestamps and datestamps. Timestamps define an era spanning 136 years, while datestamps extend over multiple eras spanning the age of the Universe to when the stars grow dim. This document clarifies the interpretation of timestamps and datestamps and their relationship with the Coordinated Universal Time (UTC) timescale used in ordinary life.
1. Introduction
As of early 2012 the Network Time Protocol (NTP) has been ticking over 30 years and remains the longest running, continuously operating application protocol in the Internet. There was some fear, especially in government and financial institutions, that NTP might cause an Internet meltdown upon the Millennium epoch, but those fears turned out to be groundless. However, the concern now is a possible meltdown when the unsigned 64-bit NTP timestamp rolls over in 2036. This document explores this issue together with the interpretation of the NTP timescale with respect to the Gregorian calendar.
It is important to make a careful distinction between the terms timescale, date, epoch, era and timestamp. A timescale is a continuum of values used to denote time in some frame of reference. While those useful for computers and networks are continuous, civil timescales may not be. For instance, in order to align the civil year with the solar year, Pope Gregory punched a 10-day hole in the Common Era (CE) in 1582. In modern times we occasionally insert a leap second to align the civil time to the solar time.
Generally, timescales are cyclic and span an era with designated beginning and span. The timescale corresponding to the Julian Era began in 4713 BCE and spans 7980 years. A date is a unique value captured as the timescale progresses and an epoch is a static date of some interest, such as the origin of the CE. In general, both dates and epochs are internal system variables with generous proportions, like 128 bits. On the other hand, timestamps are derived from dates but packed in more compact format, like 64 bits, for efficiency in transport. NTP timestamps are associated with era numbers that provide an unambiguous mapping to dates.
2. The UTC Timescale
It will be helpful in understanding the issues raised here to consider the concept of a universal timescale. The conventional civil timescale used in most parts of the world is Coordinated Universal Time (UTC), which replaced Greenwich Mean Time (GMT) many years ago. UTC is based on International Atomic Time (TAI), which is derived from hundreds of cesium oscillators in the national standards laboratories of many countries. Deviations of UTC from TAI are implemented in the form of leap seconds, which occur at intervals from a few months to several years.
For almost every computer application today, UTC represents the universal timescale extending into the indefinite past and indefinite future. We know of course that the UTC timescale did not exist prior to 1972 CE, nor the Gregorian calendar prior to 1582 CE, nor the Roman calendar prior to 54 BCE, nor the Julian Era prior to 4713 BCE, and we cannot predict exactly when the next leap second will occur. Nevertheless, most folks would prefer that, even if we can’t get future seconds numbering right beyond the next leap second, at least we can get the days numbering right until the end of reason.
3. The NTP Timescale
The NTP timescale can be implemented using a binary counter of indefinite width and with the unit seconds bit placed somewhere in the middle. The counter is synchronized to UTC such that it runs at the same rate and the units increment coincides with the UTC seconds tick. The NTP timescale is defined by 128 bits of this counter, of which the first 64 bits count the seconds and the last 64 bits interpolates the fraction of the second. The timescale covers well beyond the age of the universe with a precision well below the smallest times that can be directly measured. An implementation may choose to limit the size of the fraction field, but not less than 32 bits.
An NTP date is a sample of the counter interpreted as a two’s-complement integer. An NTP epoch is a special date distinguished by some event. The origin of the timescale, called the prime epoch (epoch 0) corresponds to 0h, 1 January 1900. Positive values represent times after the prime epoch; negative values represent times before then. Conversion between any calendar date format and NTP format is done by computing the seconds and fraction difference between the given date and the NTP prime epoch; the 128-bit signed value is the NTP date.
An NTP timestamp is a truncated NTP date expressed as an unsigned 64-bit integer including the low order 32 bits of the seconds field concatenated with the high-order 32 bits of the fraction field. This format can represent the 136 years from 1900 to 2036 with a precision of 232 ps. As will be shown later, ranges beyond these years require an era number which is the high-order 32 bits of the seconds field of the associated date.
The most important thing to observe about the NTP timescale is that it knows nothing about days, years or centuries, only the seconds and fraction relative to the prime epoch. Table 1 illustrates the correspondence between calendar date, Julian day number (JDN), NTP date, NTP era and NTP timestamp. Prior to 15 October 1582 CE, JDN years are reckoned in 365.25 days; after that, JDN years are reckoned in the Gregorian calendar. Most historians and Julian calculators do this to avoid Pope Gregory’s ten-day hole.
| Calendar Date |
JDN |
NTP Date |
NTP Era |
NTP Timestamp |
| 1 Jan 4713 BC |
0.5 |
-208,657,814,400 |
-49 |
1,795,583,104 |
| 1 Jan 1 CE |
1,721,426.5 |
-59,926,608,000 |
-14 |
202,934,144 |
| 15 Oct 1582 |
2,299,161.5 |
-10,010,304,000 |
-3 |
2,874,597,888 |
| 1 Jan 1900 |
2,415,021.5 |
0 |
0 |
0 |
| 1 Jan 1970 |
2,440,588.5 |
2,208,988,800 |
0 |
2,208,988,800 |
| 1 Jan 1972 |
2,441,318.5 |
2,272,060,800 |
0 |
2,272,060,800 |
| 7 Feb 2036 |
2,464,731.5 |
4,294,944,000 |
0 |
4,294,944,000 |
| 8 Feb 2036 |
2,464,732.5 |
4,295,030,400 |
1 |
63,104 |
| 1 Jan 3000 |
2,816,788.5 |
34,712,668,800 |
8 |
352,930,432 |
Table 1. NTP Dates
The following notes are intended to clarify what may seem to be odd features about Table 1.
-
The JDN day numbers include the fraction 0.5 day or 12 h. This is because the JDN day starts at noon, while all other days in the table start at midnight.
-
While the Unix timescale is not shown directly in the table, the correspondence between the NTP and Unix timescales is determined only by the constant 2,208,988,800. This is the number of Gregorian seconds from the NTP prime epoch 0h, 1 January 1900 to the Unix prime epoch 0h, 1 January 1970.
-
A careful reader might question the numbering system on and near the origin of the Common Era (CE) 0h, 1 January 1 CE. Since there is no year zero or day zero in the Roman calendar, day zero in this calendar coincides with 0h, 1 January 1 BCE.
Note the correspondence between the NTP date on one hand and the NTP era and timestamp on the other. The signed era number provides the base epoch in multiples of 232 s and the unsigned timestamp the offset in that era. Conversion between date and era-timestamp formats can be done by simple cut and paste requiring no arithmetic operations.
The NTP timescale is almost never used directly by system or application programs. The generic Unix kernel keeps time in seconds and microseconds (timeval) or seconds and nanoseconds (timespec). These provide both time of day and interval timer functions.
Most Unix kernels implement the timeval and timespec functions using two signed 32-bit integers, one representing the seconds since Unix life began at 0h, 1 January 1970, and the other the microseconds or nanoseconds of the second. In practice, the seconds integer changes sign in 68-year intervals, the next of which will happen in 2038. How the particular Unix system copes with this epoch is of concern, but is beyond the scope of discussion here.
The most probable solution when 2038 comes near is to replace the 32-bit seconds field of the system clock with a 64-bit field, and some kernels, including Digital Alpha, have already done that. Certainly a 64-bit integer can be used in the NTP software, but this cannot be used in packet headers exchanged over the network, as the timestamp fields contain only 64-bits and cannot be changed without causing awkward compatibility issues, especially as some provision would have to be made to operate with both 32-bit and 64-bit fields.
4. The NTP Era
As required by the NTP specification, the NTP reference implementation operates with four 64-bit raw timestamps to calculate both the clock offset and roundtrip delay. The only arithmetic operation permitted on raw timestamps is subtraction, which produces signed 63-bit timestamp differences from 68 years in the past to 68 years in the future. When computing timestamp differences and the timestamps are in the same era, the differences can be calculated directly. If not, in all credible cases the two eras will be adjacent; that is, if one timestamp is in era n, the other will be in either era n or n + 1.
Consider the case in Figure 1, where timestamps are represented as years mod 136. Server clock S is set to 2056 (timestamp 20 in era 1), while the client clock C is set to 2006 (timestamp 106 in era 0).
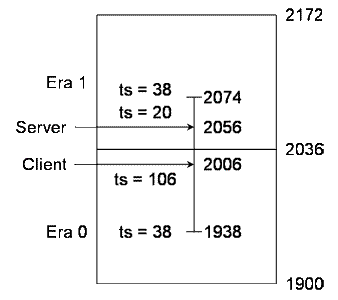
Figure 1
If S is within 68 years of C = 2006, S can be anywhere between 1938 (timestamp 38 in era 0) and 2074 (timestamp 38 in era 1). If, as in the figure, S and C are expressed as datestamps, the offset S - C = 2056 - 2006 = 50 years. However, if S and C are expressed as timestamps, as in the white paper NTP Timestamp Calculations, the offset is S +(-C) = 20 + (136 - 106= 50) mod 136 years. Thus, even if the timestamps span adjacent eras, the offset compuation is correct.
To convert system time in any format to NTP format requires only that the number of seconds s from the prime epoch to system time be determined. The era number is s / 232 and the timestamp is s mod 232. To convert from NTP era number and timestamp to system time requires only the calculation s = 232 * era + timestamp to determine the number of seconds since the prime epoch.