Timestamp Capture Principles
Last update: June 24, 2022 21:25 UTC (3a8d52d62)
from Wizard of Oz, L. Frank Baum
Ya gotta salute the principles.
David L. Mills and Stuart Venters
Table of Contents
Abstract
This document summarizes methods to achieve precise timestamp methods when exchanging Network Time Protocol (NTP) packets between servers and clients. The discussion includes the definition and measurement of statistical evaluators, as well as classification of timestamp capture methods involving softstamps, drivestamps and hardstamps.
1. Introduction
Over the 30 years NTPv4 and its predecessors have evolved, accuracy expectations have improved from 100 ms to less than 1 ms on fast LANs with multiple segments interconnected by switches and less than a few milliseconds on most campus and corporate networks with multiple LANs interconnected by routers. However, the ultimate accuracy limit for typical workstations and PCs of today is a few microseconds with a GPS receiver, PPS signal and kernel PPS support.
Improving the expected NTP accuracy to this level and beyond on LANs will require improved hardware and software technology. In principle the ultimate accuracy is limited only by the 232-ps resolution of the NTP timestamp format or about the time light travels three inches.
One of the main strengths of NTP is that it has been, and will continue to be, implemented in a wide variety of scenarios with significantly different available resources and accuracy requirements. Furthermore, timekeeping is not an exact science. No implementation provides perfect time. As such, this white paper proposes a timestamp scheme which is not an implementation requirement, but rather a specification for a model in which specific schemes can interoperate without significant loss of accuracy.
2. Application Clock Interface
The system clock interface (SCI) is the only source of time used by the NTP process and dependent applications. In Unix operating systems the SCI provides two data types, timeval (gettimeofday()) andtimespec (getclock()). Both data types represent the time in seconds past 0h, 1 January 1970. In timeval format the second is represented in microseconds, while in timespec format the second is represented in nanoseconds. In either format, the Unix time must be converted to an NTP data type before use by NTP application programs.
As described in the white paper NTP Timestamp Calculations, there are two NTP data types, datestamp and timestamp. Datestamps have 128 bits, including a 64-bit seconds field followed by a 64-bit fraction field. Timestamps have 64 bits, including a 32-bit seconds field followd by a 32-bit fraction field. The datestamp is relative to the base epoch, 0h, 1 January 1900. The timestamp data type is relative to the era number, as described in the white paper The NTP Era and Era Numbering. For the purposes of this section, either data type is acceptable.
The NTP on-wire protocol reads the SCI on two occasions: when a packet arrives and when a packet departs. In either case the SCI is subject to operating system and hardware latencies. The operating system latency typically involves a context switch in order to map the kernel address space, as well as hardware latencies to either lock the system clock variable or read the clock registers.
The SCI is not always directly usable by the NTP process and applications, and often must be augmented by a wrapper called the application clock interface (ACI). This interface provides additional functionality in order to conform to rules established by the computer science theory community and to provide additional resilience to hostile attacks. The interface conforms to the following rules.
- The values returned by the ACI must be monotone-definite; that is, every read request must return a value greater than the previous read request. This is necessary to conform to Lamport’s happens before relation and to achieve a partial order from a technical sense.
- Notwithstanding the above, a sequence of ACI reads as fast as possible must not advance the apparent reading beyond real time; that is, successive readings must not “run away”, causing the clock to advance without bound.
- In the values returned by the ACI, nonsignificant bits should be filled with a random bit string. This is to minimize the possibility of an intruder synthesizing an acceptable reply to a request.
The ACI wrapper is most useful as a library routine linked with the NTP process and with applications dependent on NTP synchronization. The ACI algorithms and data structures are described in following sections.
2.1 Structural Metrics
There are three important metrics in the ACI. The precision ρ is the time taken to read the system clock by an application program, typically in the hundreds of nanoseconds in modern processors and operating systems. The resolution ζ is the minimum increment that can be distinguished in successive clock readings, typically from a few nanoseconds to tens of milliseconds in different operating systems and supporting hardware. The entropy π is the number of significant bits returned in a SCI call. This number depends on the resolution of the hardware clock and the Unix clock data type. For a timeval data type with microsecond resolution, this number is 20 bits; for a timespec data type with nanosecond resolution, this number is 29 bits.
The metrics can be measured when the NTP process begins and before regular operation. It is important to observe that the measurement technique makes no a-priori assumptions about the machine hardware or operating system. The technique is to read the SCI in a continuous loop and record the number of completions in a measurement interval in the order of one second. The ρ metric is the measurement interval divided by the number of SCI completions during the interval. The ζ metric is the measurement interval divided by the number of SCI changes during the interval. For interpolated SCI using the TSC in Intel systems or the PCC in Alpha systems, the ζ is equal to ρ; for non-interpolated SCI, ζ is the interval between ticks of the system clock, which can be up to tens of milliseconds. Measurement of the π metric requires a special algorithm, as described below.
2.2. Application Clock Interface Algorithm
An algorithm to read the system clock consistent with the above rules is as follows. The algorithm assumes the SCI returns monotone values, but not necessarily monotone-definite. Thus, successive calls on the SCI might return the same values.
Let the persistent variable u represent the last value returned by the SCI and v represent the last value returned by the ACI algorithm. The algorithm works as follows.
-
If the value returned by the SCI is different than u, replace u and v by this value and return v as the algorithm result.
-
If the value returned by the SCI is the same as u, set v = v + ρ and return v as the algorithm result.
Clearly, the algorithm result is monotone-definite and cannot “run away” as the result of repeated calls, no matter how often.
2.3. Entropy Mask Algorithm
In order to enhance intruder resistance, it is necessary to modulate the low-order nonsignificant bits of the SCI reading with a random bit string. However, identifying which low-order bits are nonsignificant may not be straightforward. The algorithm described in this section does this by measuring the entropy of each bit of the SCI reading and constructing a bit mask covering the nonsignificant bits. While the description assumes a 32-bit timestamp fraction, the same algorithm applies for a 64-bit datestamp fraction.
The algorithm proceeds in the same steps as the ACI algorithm above. Let x, y and z be persistent 32-bit integer variables and d be a 32-element array of integers, all initialized at zero. The x holds the seconds fraction returned by the previous SCI call, while y holds the seconds fraction returned by the current call. After each call to the SCI, set z equal to the exclusive-OR of x and y, then set x equal to y.
The entropy array d is updated in the following step. Consider each bit i of z:i (i = 0, 1, …, 31). If z:i is equal to 1, increment d[i]; otherwise, do nothing. This continues over the interval processed by the ACI algorithm. Then, the d array is normalized, so that the sum of the elements is equal to 1.
The entropy and entropy mask are determined as follows. Scan the d[i] entries in the order (i = 31, 30, …, 0) and stop at the first element k such that d[k] is greater than a threshold to be determined later. The value k is the entropy π, while value b = 31 − k is the size of the entropy mask of 1 bits. However, there is an additional restriction. The size of the entropy mask can not exceed the size of the precision mask defined as log2ρ.
During regular operation after the ACI and entropy mask algorithms are complete, each call to the ACI is exclusive-ORed by a right-adjusted string of b random bits. The result maximizes the entropy of the reading while conforming to the rules described at the beginning of this section.
3. Improving the System Clock
In a program to improve timekeeping accuracy and precision, the first thing to look at is the system clock maintainted by the operating system kernel. In current technology and without introducing external hardware components, use the precision kernel described elsewhere. However, there are ways to further improve performance, as described in this section.
For historic reasons, the clock is implemented as two 32- or 64-bit words; the high-order word counts the seconds, while the low-order word counts the modulus of the second. Modern systems use moduli of 106 (microseconds), 109 (nanoseconds), 232 (fraction for 32-bit word size) or 264 (fraction for 64-bit word size). The first two moduli are used by Unix systems, while the last two would be appropriate should the system clock be implemented in hardware. As aside, DEC systems (VAX) increment the clock in nanoseconds, while IBM (VMS) systems increment the clock in microseconds at bit 52 of a 64-bit word. The result is that bit 31 rolls over at something close to but not exactly one second. Apparently believing in time dilation, IBM calls this a megamicrosecond.
A hardware clock oscillator and counter/divider provide interrupts at regular intervals called ticks by computer engineers and jiffies by computer scientists. At each interrupt the low-order system clock word is incremented by the modulus multiplied by the tick in seconds. When the incremented value equals or exceeds the modulus, the high-order word is incremented by one and the modulus is subtracted from the low-order word. Note that the resolution without interpolation is by construction equal to the tick.
There are considerable differences between systems about the design parameters. Various machines, past and present, have used clock frequencies off several MHz and timer frequencies (reciprocal of the tick) of 50/60 Hz, 100 Hz, 256 Hz, 1000 Hz and 1024 Hz. At one time in the past kernel implementors were reluctant to use timer frequencies that do not divide the modulus; e.g., 1024 Hz does not divide 109, but does divide 232. This was because early kernels accumulated the number of ticks, not the tick values themselves.
Conventional Unix kernels store the tick as a 32-bit fixed value in microseconds or nanoseconds. In the precision kernel this value is a variable proportional to the frequency computed by the clock discipline. For a frequency resolution of 1 ns/s, 32 bits is not enough, especially at timer frequencies of 1000 Hz or greater. For this reason the precision kernel uses a 64-bit tick value in nanoseconds with the decimal point in the middle.
Most modern machines have a processor cycle counter (Intel TSC, DEC Alpha PCC), which can be used to interpolate the tick with high resolution. However, there is a subtle complication when multiple processors are involved. Typically, these machines have a separate cycle counter for each processor and implement the timer components in a separate support chip. In systems known by this author, the timer interrupt is vectored to one processor. However, a request to read the system clock could happen in any processor.
On a 64-bit machine the cycle counter c for any processor can be converted to seconds fraction in three steps: (1) multiply the low-order 32 bits of c by a factor d to be determined later, (2) shift right 32 bits and (3) store as the low-order word. This avoids an integer divide operation, which along with floating point arithmetic is to be avoided in kernel code. The factor d is
d = 232 r / f
where r is the modulus and f is the processor clock frequency, which must be measured to very close tolerances in the order of 1 ns/s.
In practice, f is measured at relatively infrequent intervals, like a second or two, as the change in c over the interval divided by the change in system time t over the interval. As the system time at a timer interrupt is exact, the frequency and thus d can be determined to a high degree of accuracy. For instance, with r = 109 and f = 3.4 GHz, d = 1.2632x109. For frequency adjustment, this provides a resolution of about 1 ns/s.
On a 32-bit machine this gets much more messy. Now we have to read the clock in two steps, so either a synchronizing primitive like spin lock is necessary or we can use Lamport’s rule. Brieftly put, in Lamports rule the program reads the high-order word, then the low-order word and finally the high-order word again. If the first and second high-order words disagree, do this again until they do.
4. Requirements and Principles of Hardware Timestamping
In practice, the precision kernel delivers about the best accuracy and precision available, assuming external synchronization sources are of sufficient quality are available. In general, and even with faster hardware and network links, improved accuracy can only be achieved with minute attention to the residual errors that occur in normal operation, including systematic and stochastic delay variations due to competing network traffic and operating system scheduling.
Stochastic errors are generally mitigated by the NTP mitigation and discipline algorithms. In general, these errors can be further reduced using some kind of hardware assist or special provisions in the network interface card (NIC) or device driver. Improved means to do this are discussed in this section.
To better understand the issues, consider the ultimate case where the server and client implement clocks that can be read with exquisite accuracy. The object is to measure the time offset of a server relative to the client.
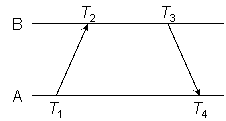
Figure 1
As shown in Figure 1, the NTP on-wire specification uses what is called here the reference timestamps T1, T2, T3, and T4, respectively called the origin, receive, transmit and destination timestamps. T1 and T4 are struck by peer A from its clock, while T2 and T3 are struck by peer B from its clock. The object of the protocol is to determine the time offset of B relative to A and the roundtrip delay ABA:
offset θ = [(T2 − T1) + (T3 − T4)] / 2 (Example 1)
delay δ = (T4 − T1) − (T3 − T2) (Example 2)
The precision to which the offset and delay can be calculated depends on the precision with which the timestamps can be struck. In general, it is best to strike the timestamps as close to the physical media as possible in order to avoid various queuing and buffering latencies. In this case the physical data media block is properly called a frame, but for clarity in the following discussion and for consistency with other documents in this collection, it will be called a packet.
Timestamps are categoized by the point in the code flow that they are captured. Softstamps are captured in the mainline code before a packet is sent or after a packet is received. Drivestamps are captured in the packet interrupt routine after a packet is sent or received. Hardstamps are captured by the hardware upon passage of a designated symbol in the media interface. This document does not consider hardstamps, as this requires special purpose network interfaces unavailable in the general population. By default, the NTPv4 reference implementation uses softstamps for transmitted packets and drivestamps for received packets. If interleaved mode is enabled in symmmetric and broadcast modes, drivestamps are used for transmitted packets as well. Additional information on interleaved modes is in the white paper Analysis and Simulation of the NTP On-Wire Protocols.
The timestamp scheme used by the NTP reference implementation attempts to approximate the reference timestamps as follows:
-
When interleaved mode is not enabled, T1 and T3 softstamps are struck by the output packet routine just before the message digest (if used) is calculated and the buffer is passed to the operating system. Applicable latencies include digest overhead, output queuing, operating system scheduling, NIC buffering and possibly NIC retransmissions. If interleaved mode is enabled, but only in symmetric and broadcast modes, T1 and T3 drivestamps are struck in the transmit interrupt routine.
-
In all modes, T2 and T4 drivestamps are struck just after the input packet interrupt routine and before the buffer is queued for the input packet routine. Applicable latencies include NIC buffering, interrupt processing and operating system scheduling, but not input queuing.
If these latencies can be avoided, the remaining latencies are due only to network propagation, packet transmission and network queues. Inspection of Example 1 shows that the best accuracy is obtained when the delays on the outbound path T1 → T2 and inbound path T3 → T4 are statistically identical; in this case we say the delays are reciprocal. Further refinement demonstrated later in this section shows that, if the reciprocal delays differ by x seconds, the resulting offset error is x/2 seconds.
Lack of reciprocity is due to two causes, different delays on the outbound and inbound paths and where in the packet the timestamps are struck. If the overall data rate and packet lengths are not the same on both directions, errors will result. If the transmitter and receiver choose different points in the packet to strike a timestamp, errors will result. What happens depends on the hardware and software design, as described below.
There are many workable schemes to implement timestamp capture. Using a different scheme at each end of the link is likely to result in a lack of reciprocity. The following provisions apply:
-
The capture location should be relative to the physical media at some point in the packet that can be recorded by the hardware, firmware and software.
-
A preamble timestamp is struck as near to the start of the packet as possible. The preferred point follows the last bit of the preamble and start-of-frame (STF) octet and before the first octet of the data.
-
A trailer timestamp is struck as near to the end of the packet as possible. On transmit this follows the last octet of the data and before the frame check sequence (FCS); on receive this follows the last octet of the FCS. The reason the capture locations necessarily differ is due to the hardware and protocol design. (Note: A sufficiently large and complex FPGA might be able to deliver the timestamp at the same point as the transmitter, but this doesn’t seem worth the trouble.
-
In addition to the timestamps, the NIC and/or driver must provide both the nominal transmission rate and number of octets between the preamble and trailer timestamps. This can be used by the driver or application to transpose between the preamble and trailer timestamps without significant loss of accuracy. The transposition error with acceptable frequency tolerance of 300 PPM for 100-Mb Ethernets and nominal 1000-bit NTP packet is less than 3 ns.
As shown later in this section, the best way to preserve accuracy when single or multiple network segments are involved, some possibly operating at different rates, is the following:
-
The propagation delay measured from the first bit sent in a packet to the first bit received on each direction of transmission must be the same. This is called the reciprocity rule.
-
T1 and T3 must be struck from the preamble timestamp.
-
T2 and T4 must be the struck from the trailer timestamp.
Whatever timestamping scheme is developed, it should allow interworking between schemes so that every combination of schemes used by the server and client results in the highest accuracy possible. As shown later, this can be achieved only using the above rules.
5. Timestamp Transposition
With the above requirements in mind, it is possible to select either the preamble or trailer timestamp at either the transmitter or receiver and to transpose so that both represent the same reference point in the packet. The natural choice is the preamble timestamp, as this is considered the reference timestamp in this document and is consistent with IEEE 1588 and likely to be supported by available hardware. With and without transparent bridges or boundary clocks, accuracies with NTP will be of the same order as 1588. However, as shown below, this does not work if there is a bridge or router between the server and client and both operate at different rates.
As shown below, with driver timestamps the transmitter must transpose the trailer timestamp to the preamble timestamp according to the respective data rate and packet length. With hardware timestamps the receiver must transpose the preamble timestamp to the trailer timestamp.
An NTP packet (about 1000 bits) is 1 μs on a 1000-Mbps LAN, 10 μs on a 100-Mb LAN and 650 μs on a T1 line. As shown later, in order to drive the residual NTP offsets down to PPS levels, typically within 10 μs, the reciprocal delays must match within 10 μs. if the reciprocal transmission rates and packet lengths are the same to within 10 μs, or one packet time on a 100-Mbps LAN, the accuracy goal can be met.
Example
- NTP servers macabre and mort are identical Intel Pentium clones running FreeBSD and synchronized to a GPS receiver via a lightly loaded 100-Mbps LAN and share the same switch. Each server shows nominal offset and jitter of about 25 μs relative to the other and the GPS receiver. Delays of this order normally would be considered reciprocal. Each server shows a roundtrip delay of about 140 μs with the other. Since 40 μs (four LAN hops) is due to packet transmission time, the remaining 100 μs is shared equally by each server due to buffering in the operating systems and NICs.
Further improvement in accuracy to the order fo the PPS signal requires hardware or driver assist as described later.
6. Error Analysis
The analysis so far does not account for various statistical latencies, nor does it accounts for systematic errors resulting from nonreciprocal network paths. The NTP code path delay and the latency to read the system clock are substantially the same on either direction, so cancel out. As previously noted, the Ethernet transceivers themselves contribute significant delays. While these delays are generally constant, additional delays can occur due to operating system and device latencies. In addition, NTP traffic typically competes with other network traffic causing additional statistical latencies. However, the important assumption about these delays is that the probability distribution for the reciprocal paths are substantially the same.
In Figures 1 and the following, upper case variables represent the reference timestamps used in Example 1 and Example 2. In the following, lower case variables represent the actual timestamps struck by the hardware or software. The on-wire protocol uses the actual timestamps in the same fashion as Example 1 and Example 2. The object is to explore the possible errors that might result from different timestamp strategies.
In the NTP reference implementation the t1 and t3 (transmit) softstamps are struck before computing the message digest (if used) and handing the packet buffer to the operating system, which results in various digest, queuing and buffering latencies represented by the random variable εt. In Unix, for example, the user-space buffer is ordinarily copied to kernel-space buffers (mbufs) which then are passed to the NIC. However, modern NICs of the PCNET family can use a chain of hardware descriptors, one for each buffer, and can DMA directly from a user-space buffer to an internal 16K FIFO, shared between the transmit and receive sides, and separate PHY buffers for each side. The NIC driver manages the FIFO and PHY scheduling to achieve maximum throughput, but might not be sensitive to latencies. The NIC driver manages the FIFO and PHY scheduling to achieve maximum throughput, but might not be sensitive to latencies.
The random variables εt and εr represent samples from a continuous distribution, However, the clock discipline algorithm averages many measurements to determine the clock adjustment. Therefore, a useful simplification in this document is to represent the random variables by their expectations. Thus, we assume T1 = t1 + εt and T3 = t3 + εt.
In anticipation of a packet arrival, the NTP implementation allocates an input buffer in user space. When a complete packet (chain of kernel mbufs) arrives, the driver copies the mbufs to the buffer. The t2 or t4 (receive) drivestamp is struck from the system clock and copied to the buffer. The drivestamp is delayed by various device driver and operating system latencies represented by the random variable εr. Thus, T2 = t2− εr and T4 = t4 − εr. The interrupt routine then copies the drivestamp to a preallocated field in the buffer.
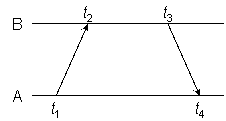
Figure 5
As shown in Figure 5, the NTP on-wire protocol performs the same calculations as Example 1 and Example 2 but using the actual timestamps. After substitution we have
θ = {[(T2− εr) − (T1 + εt)] + [(T3 + εt)− (T4−εr)]} / 2
which after simplification is the same as Example 1. On the other hand,
δ = [(T3 + εt) − (T2− εr)] − [(T4− εr)− (T1 + εt)]
results in an additional delay of 2(εt + εr).
While these equations involve random variables, we can make strong statements about the resulting accuracy if we assume the probabilty distributions of εt and εr are stationary over the averaging time of the clock discipline algorithm. We conclude that, as long as the delays on the reciprocal paths are the same and the packet lengths are the same, the offset is as in Example 1 without dilution of accuracy. There is a small increase in roundtrip delay relative to Example 2, but this is not ordinarily significant.
The principal remaining terms in the error budget are nonreciprocal delays due to different data rates and nonuniform transposition between the preamble and trailer timestamps. The errors due to such causes are summarized in following sections.
7. Reciprocity Errors
The above analysis assumes that the delays on the outbound and inbound paths are the same; that is, the paths are reciprocal. This is assured if the propagation delays are the same, the transmission rates are the same and the packet lengths are the same. In the NTP on-wire protocol all packets have the same length. If we assume the transmission rates are the same, the only difference in path delays must be due to nonreciprocal transmission paths. This often occurs if one way is via landline and the other via satellite. It can also occur when the paths traverse tag-switched core networks.
Some idea of the errors introduced by nonreciprocal paths is illustrated in Figure 6, where the reference timestamps represent a network with zero delays and then add an outbound delay dAB and inbound delay dBA.
Figure 6
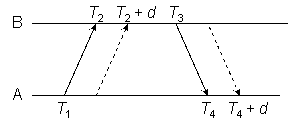
As shown in Figure 6, the NTP on-wire protocol performs the same calculations as Example 1 and Example 2 using the reference timestamps but ignoring the latencies discussed in the preceding section. After substitution we have
θ = {[(T2 + dAB) − T1] + [T3 − (T4 + dBA)]} / 2
which after simplification results in an error of (dAB - dBA) / 2. On the other hand,
δ = [(T4 + dBA) − T1] − [T3 − (T2 + dAB)]
results in a roundtrip delay of dAB + dBA as expected.
Example
- Sun Ultra pogo and Intel Pentium deacon, both synchronized to PPS sources showing typical offset and jitter less than 5 μs. Both are clients of each other via bridged 100-Mbps LAN segments so the roundtrip delay between the NICs is 40 μs for 1000-b packets and four hops. The roundtrip delay measured by either machine is about 400 μs and the jitter estimated at 25 μs. The measured offset of pogo relative to rackety is 89 μs, while the measured offset of rackety relative to pogo is -97 μs.
The fact that the two machines are synchronized closely to the PPS signal and the measured offsets are almost equal and with opposite sign suggests that the two paths are nonreciprocal. Of the measured roundtrip delay, 40 μs is packet transmission times; the remaining 360 μs must be due to buffering in the operating system and NICs. From the above analysis, the offset error is consistent with one path having about 200 μs more overall delay than the other. Of the 360 μs roundtrip delay, this suggest rackety accounts for 80 μs leaving 280 μs for pogo.
8. Hardware Timestamping
There are two ways to reduce the queuing and buffering latencies: hardware timestamps and driver timestamps. An example of hardware timestamps is IEEE 1588, in which an event such as the passage of the Ethernet STF octet, latches an internal NIC counter. We assume the internal counter is disciplined by means other than NTP, e.g., IEEE 1588. This approach requires at least two latches, one for the transmit side and the other for the receive side. In addition, the driver must read a latch before another STF comes along, or the latches must be buffered in a FIFO.
With application to NTP, the latch can be read by the Ethernet driver, converted to NTP format and inserted following the packet data. With Unix systems this ordinarily would be saved in the mbuf chain. On output, the driver reads the latch, converts to NTP format and does one of two things. It can provide the information in the form of a pseudo-input buffer or use some form of interprocess message, both of which are awkward. Either method avoids substantially all queuing and buffering latencies in the software design.
With hardware timestamps the actual preamble timestamps are struck from hardware and are thus identical to the reference timestamps. However, t1 and t3 are valid only if the packet is the final successful transmission. We conclude that, as long as the transmission rates on the reciprocal paths are the same, the offset and delay can be computed as in Example 1 and Example 2 without dilution of accuracy.
9. Driver Timestamping
With driver timestamps a trailer timestamp is struck from for each packet sent or received. The timestamp is available only at driver interrupt time; that is, at the end of the packet and before the FCS on transmit and after the FCS on receive. Assuming the timestamps can be passed up the protocol stack as in hardware timestamping, this avoids most of the output queue and kernel buffer latencies of the software design.
With driver timestamps there is a delay d between the reference timestamp (preamble timestamp) and the trailer timestamp corresponding to the packet transmission time. Assuming this is the same for the reciprocal paths, t1 = T1 + d, t2 = T2 + d, t3 = T3 + d, and t4 = T4 + d. In this case we neglect the time to transmit the checksum, which is 32 ns for 1000-Mb LANs and 320 ns for 100-Mb LANs. Then,
θ = {[(T2 + d) − (T1 + d)] + [(T3 + d) − (T4 + d)]} / 2
which after simplification is the same as Example 1. On the other hand,
δ = [(T4 + d) − (T1 + d)] − [(T3 + d) − (T2 + d)]
which after simplification is the same as Example 2. We conclude that, as long as the transmission rates on the reciprocal paths are the same and the packet lengths are the same, the offset and delay can be computed as in Example 1 and Example 2 without dilution of accuracy.
10. Interworking Errors
Recall that reference timestamps are struck at the beginning of the packet on both transmit and receive and so are invariant to the transmission rates and packet length. However, trailer timestamps are struck at the end of the packet, which is later than the reference timestamps depending on the transmission rate and packet length. Let the delay between the reference and trailer timestamps be d. Then, consider what happens when interworking between various combinations of software, hardware and driver timestamps without proper transposition.
Let A use hardware timestamps and B driver timestamps. Then,
θ = {[T2 − (T1 + d)] + [T3 − (T4 + d)]} / 2
results in an offset error of −2d, while
δ = [(T4 + d) − (T1 + d)] − (T3 − T2)
results in no error.
Let A use driver timestamps and B software timestamps. Then,
θ = {[(T2 + d) − (T1 + d)] + [T3 − (T4 + d)]} / 2
results in an offset error of −d, while
δ = [(T4 + d) − (T1 + d)] − [T3 − (T2 + d)]
results in a delay increase of d. Other combinations are possible.
11. Store and Forward Delay Errors
Consider a scenario with two LAN segments connected by a switch or router, where one segment operates at 10 Mb and the other at 100 Mb. Even with hardware timestamps errors can occur due to the different packet transmission times.
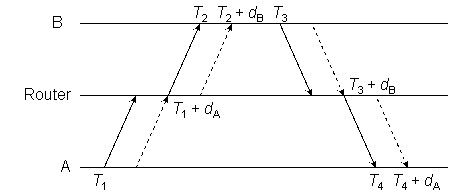
Figure 7
In Figure 7 let dA be the packet time for A and dB be the packet time for B. The router sends the packet to B only after the packet has been received from A, assuming the switch is not capable of cut-through switching. With hardware (preamble) timestamps,
θ = {[(T2 + dA) − T1] + [T3 − (T4 + dB)]} / 2
results in an offset error (dA − dB) / 2. As above, if dA = dB, there is no offset error. On the other hand,
δ = [(T4 + dB) − T1)] − [T3 − (T2 + dA)]
results in a delay increase of dA + dB.
If a software timestamp scheme is chosen for the above example, then,
θ = {[(T2 + dA + dB) − T1] + [T3 − (T4 + dA + dB)]} / 2
results in a zero offset error. On the other hand,
δ = [(T4 + dA + dB) − T1)] − [T3 − (T2 + dA + dB)]
results in a delay increase of 2(dA + dB).
From this we can conclude that it’s not only the timestamping schemes at A and B which must match, some consideration must also be given to the forwarding behavior of the switches connecting A and B when the link speeds differ. Using the preamble timestamp as the transmit timestamp and the trailer timestamp as the receive timestamp solves this problem.
12. Nonreciprocal Rate Errors
A transmission path will typically be two or more concatenated network segments that might operate at different rates. The above analysis assumes that the transmit and receive rates are the same for each network segment, even if different on different segments. The problem considered in this section is when the transmit and receive rates is different on some segment. This is a common condition on space data links.
Assume the packet transmission time on a particular segment is δ = p + L / r, where p is the propagation delay, L the packet length in bits and r is the transmission rate in bits per second. Now consider the total delay δ over a path consisting of concatenated segments,
δ = (p1 + L / r1) + (p2 + L / r2) + … + (pn + L / rn)
where n is the number of segments on the path. If we assume the outbound and return paths traverse the same segments in reverse order, the total delay on each direction will be the same. If the timestamps are taken as described previously, the delays are reciprocal and accuracy is not diluted.
Let δ21 be the total delay on the outbound path from the client to the server, then above can be written
δ21 = sum(pi) + L sum(1 / ri) (i = 1…n)
where n is the number of network segments. Let r21= 1 / sum(1 / ri) be the overall outbound transmission rate, where i indexes the outbound segments. Let r34= 1 / sum(1 / ri) be the overall inbound transmission rate, where i indexes the inbound segments. Then, L / r21 is the overall outbound delay and L / r34 is the overall inbound delay.
In the case of space data links, the delay from the first symbol of the RF signal to the timestamp capture point, the ASM octet, is primarily due to Reed-Solomon encoding and interleaving. The delay is typically included in the light time propagation delay. Also, the message bit rate is typically one-half the channel bit rate due to convolutional encoding. The net channel delay and bit rate are determined from the RF channel parameters, which are known in advance. Thus, the clock offset is
θ = {[(T2 + L / r21) − T1] + [T3 − (T4 + L / r34)]} / 2
which as expected results in no delution of accuracy if the overall inbound and outbound rates are the same. If not, a workable remedy is to subtract the rate term from the corresponding receive T2 and destination T4 timestamps before tthey are stored.
Where necessary, the roundtrip delay can be determined as
δ = [(T4 + L / r34) − T1] − [T3 − (T2 + L / r21)]